数学大神陶哲轩用GPT-5解决数学难题：只用了29行Python代码

（由多段落组成）：

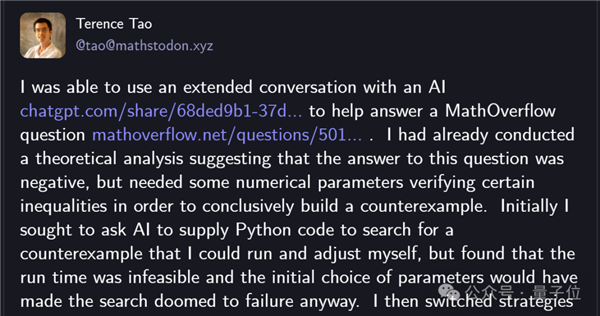
近日，国际知名数学家陶哲轩再次借助人工智能技术，在数学研究中取得关键突破。他在最新发布的社交媒体帖子中坦言，此次若没有AI的协助，完成相关任务将耗费数小时的人工编码与调试时间，甚至可能根本不会尝试当前这一高效的解决路径。

陶哲轩此次面对的问题源自专业数学问答平台MathOverflow：序列 lcm(1,2,…,n) 是否为“高度丰数”（Highly Abundant Numbers, HA）的一个子集？该问题本质上是两个特殊数列之间的关系验证——一个是前n个自然数的最小公倍数序列，另一个则是所有约数之和大于任何小于它的正整数的“高度丰数”序列。例如，lcm(1,2)=2、lcm(1,2,3)=6、lcm(1,2,3,4)=12……而像1、2、4等数因其约数和显著领先，也被归类为高度丰数。初步观察显示这些最小公倍数似乎都属于高度丰数，但是否恒成立？

通过理论分析，陶哲轩已判断答案应为“否”，但要彻底证明这一点，必须找到一个具体的反例，而这需要大量数值计算和参数搜索。传统方式下，这类工作不仅耗时且容易出错。然而，这次他选择引入GPT-5作为协作工具，仅用几次自然语言对话便高效推进了整个过程。

起初，他让GPT-5直接生成用于搜索反例的Python代码。虽然模型在约一分多钟后输出了一段完整程序，但实际运行发现其效率低下、初始参数设置不合理，难以收敛结果。于是陶哲轩调整策略，转而采用分步引导的方式，将复杂问题拆解成多个小目标，逐步引导AI进行启发式推理与参数优化。经过几轮交互，GPT-5最终成功提供了可行的候选参数。

为进一步验证准确性，陶哲轩使用由AI生成的一段仅29行的简洁Python脚本进行了独立复现。这段代码逻辑清晰、结构紧凑，易于人工审查，且计算结果与之前的预测完全一致。更令人惊喜的是，在整个过程中，AI未出现常见的“幻觉”现象，没有产生虚假数据或错误推论，展现出极高的可靠性。

这并非陶哲轩首次利用AI辅助数学研究。今年以来，他多次公开分享AI在科研中的应用案例：9月初使用GPT-5实现Erdős问题与OEIS数据库的智能关联；5月通过GitHub Copilot快速完成函数极限证明，并在YouTube上直播演示；同月还利用AI在33分钟内完成Magma方程E1689蕴含E2的“盲证”；3月时，AI甚至帮助他识别并纠正了一个隐藏的逻辑错误，极大提升了求解效率。

在他看来，尽管AI短期内无法获得菲尔兹奖这样的顶级学术荣誉，但它正逐渐成为数学家思维过程中的“智能中介”——既能加速繁琐计算，又能激发新的研究思路。这种“人机协同”的新模式，正在重塑基础科学研究的方法论。

值得一提的是，OpenAI首席科学家Sebastien Bubeck也迅速转发了这一成果，引发科技与数学社区广泛讨论。许多人表示，这标志着人类与机器共同探索未知的时代已经到来。与此同时，OpenAI CEO山姆·奥特曼近期对GPT-5的评价也引发热议。他强调GPT-5并非颠覆性跃迁，而是渐进式迭代，呼吁公众降低对其能力的过度期待。同时，他对通用人工智能（AGI）的时间表态度趋于谨慎，更加重视安全性与可控发展。

从数学前沿到AI伦理，这场跨领域的碰撞不仅展示了技术如何赋能顶尖科研，也提醒我们：正确使用AI，远比拥有强大模型更重要。未来，随着AI工具日益成熟，或将催生更多“陶哲轩式”的创新实践，推动科学边界不断扩展。

AI辅助科研, 陶哲轩, GPT-5, 数学难题, 人机协同

本文来源： 快科技【阅读原文】